基于遗传算法和线性规划的快递包装盒下料问题研究

摘要

板材下料是多数生产制造企业的第一道工序，如何在满足客户需求的基础上实现材料利用率的提高与利润的最大化，一直是厂家关注的问题。

本文旨在通过建立系列数学模型，对企业生产包装纸箱的原材料切割方式及生产规模进行规划，使得该企业利润达到最大化。首先，本文依据遗传算法建立下料模型，确定使得原材料利用率较优的原材料切割方案，并在此基础上，建立合理的线性规划模型，求解利润最大化的最终生产方案。随后，考虑到客户需求的弹性，本文在原有线性规划模型基础上进行优化，确定部分包装可替代条件下的生产方案。最后，本文进行了进一步的分析，探究不同种类快递纸箱的需求变化对生产计划的敏感性，为企业与下游快递公司的合作提供帮助。

针对问题一，本文将生产方案的制定进行划分，先确定瓦楞板怎样切割再确定各切割方案怎样生产。首先，以瓦楞纸的最大利用率为目标，建立了以遗传算法为基础的下料模型。在保证各瓦楞纸的切割方案能够覆盖所有的包装种类的前提下，最终排布出了16种固定的切割方案，每种切割方式的平均利用率达到了94.79%。接着，在此基础上，本文根据需求量，以利润最大为目标进行整数线性规划，求得最终生产计划。具体结果为：三层纸箱总利润约为239.599元，原料利用率约为81.08%；五层纸箱总利润约为176.87元，原料利用率约为78.67%，利润总计约416.469元。

针对问题二，在明确纸箱的具体代替情况后，对前问整数线性规划模型进行改进。由于实际生产中的需求是弹性的，容积差值在一定范围内可以使用大纸箱替代小纸箱，本文在问题一的基础上，对具体的约束条件及目标函数进行优化。增加纸箱替代数量这一变量，重新进行规划求解，具体结果为：三层纸箱总利润约为243.089元，利用率约为67.78%；五层纸箱总利润约为181.425元，利用率约为79.86%。利润合计约为424.514元。

针对问题三，本文采用将各箱子的需求量依次增加10%的策略进行探究，根据问题一建立的相关模型将变动后数据代入进行求解并对利润进行比对，最终得到第1、2号箱子的需求量对生产计划最为敏感。并且总体上利润变化率基本在5%以内，最大也仅在10%左右，说明系统稳定性良好，灵敏度校验效果较好。

最后，本文对该模型的优缺点进行了分析，发现，但却可以在原材料变更、需求量变更的情况下灵活使用，适用度良好。

关键字：二维矩阵下料问题；遗传算法；整数线性规划；灵敏度分析

问题重述

问题背景

随着电商行业的蓬勃发展，物流行业对快递纸箱的数量需求越来越多[1]，且规格需求越来越复杂，导致纸箱包装生产企业面临着不小的竞争压力。如何降低成本、实现利润的最大化是当今各个纸箱包装生产企业亟待解决的问题，最大限度地节约材料，提高材料利用率是生产中提高效益的一个重要手段，在此基础上，又要制定合理的生产计划，以应对客户多变的需求。如何使原材料利用率最高、利润最大，即如何下料与如何进行生产规划，成为企业生产的重中之重。

“下料问题”[2]是把相同形状的一些原材料分割加工成若干个不同规格大小的零件的问题。在传统下料模式中面临两个问题，一是大多并不能从整体上寻求一个较优的结果，而只是依据加工形状从板材直接顺序剪切，这就会造成材料的大量浪费；二是下料切割方案分配不合理，很难定时定量定额地管理下料过程。因此，对于纸箱包装生产企业来说，合理地制定板材下料及生产方案，可以帮助企业提高材料利用率、节约生产成本，是使得企业在激烈市场竞争中站稳脚跟的关键。

问题描述

某企业使用边长分别为2.5m，2.0m，1.8m，1.5m的正方形瓦楞板为快递公司生产包装纸箱，其中三层瓦楞板成本分别为10.0，6.5，4.8，4.0元，五层瓦楞板成本为对应三层板的 1.3 倍。在切割工程中剩余的瓦楞板可以以每平米1.4元在其企业内部回收利用

问题一要求根据所给数据，确定该企业的一天内生产计划，使其利润最大。

问题二假设在容积误差 30%之内的纸箱可以以大纸箱代替小纸箱供货，要求在该给定假设的前提下求出该企业的一天内生产计划，使其利润最大。

问题三要求对问题一中的模型进行灵敏度分析，并根据结果求出需求变化对生产计划最为敏感的快递纸箱。

模型假设

本文使用数据真实有效；
不考虑瓦楞板切割工艺造成的损耗；
不考虑纸箱拼装时的板材需求；
将纸箱平面展开图视为规则矩形。

符号说明

符号	含义
$l_{i}$	第$i$号纸箱切割长度
$w_{i}$	第i号纸箱切割宽度
$m_{i}$	第i号纸箱单价
$d_{i}$	第i号纸箱需求量
$a_{j}$	第j种切割模式的瓦楞板边长
$c_{j}$	第j种切割模式的瓦楞板成本
$x_{j}$	第j种切割模式的使用次数
$m_{re}$	回收价格
$I_{i,j}$	第i种纸箱由第j种纸箱替换的个数
$A_{MN}$	$M \times N$矩阵，表示各模式生产各类纸箱的数量，$M$为需求纸箱的种类数量，$N$为生产模式的数量利润
$z$	利润

问题一模型的建立与求解

问题一的分析

问题一要求根据企业1天的订单数确定该企业的生产计划，可以划分为制定瓦楞板的下料方案、制定生产计划满足需求两个步骤。在制定瓦楞板的下料方案时，需要能够兼顾每一种需求纸箱的下料生产，以及板材利用率最大两项需求。而在制定生产计划时，则需要在考虑各项纸箱的成产计划数量大于各自的需求数量的基础之上，合理规划使得企业的利润最大化。为此，我们在第一步采用遗传算法[3]，分别为四种板材制定出共16种切割方案，在第二步，在已有的切割方式下，采用线性规划的方法根据需求量列出相关方程，并设置目标函数为纯利润，将问题数学模型化进行求解，最终得出企业该日的生产计划。

数据预处理

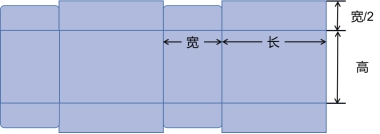
考虑到快递纸箱并非简单的立方体展开模型，其顶部与底部是由两对纸板拼合组成（图1），由图2快递纸箱的平面展开示意图可知，快递纸箱大致呈现为矩形[4]。为将问题简化，本文将展开后的纸箱形状视为规则矩形。


图1 快递纸箱示意图	图2 快递纸箱展开平面示意图

根据题中所给相关参数求出各个纸箱平面图大小如表1所示：

表1 各纸箱平面图大小

纸箱编号	需要长度	需要宽度	纸箱编号	需要长度	需要宽度
1	1660	670	7	720	290
2	1540	530	8	640	250
3	1280	480	9	600	240
4	1080	420	10	540	210
5	920	360	11	460	190
6	800	330	12	420	170

遗传算法模型的建立

为了便于生产且简化运算，首先我们使用了遗传算法对瓦楞纸的切割方式做出了规划。

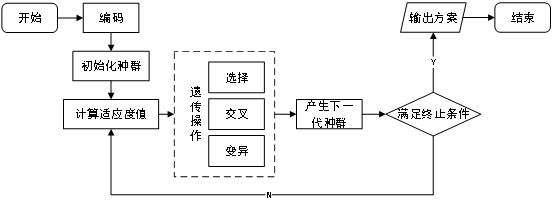
遗传算法(Genetic Algorithm, GA)是一种通过模拟自然生命现象，借鉴生物界的自然选择和进化机制演化而来的随机搜索方法，是基于生物进化和随机选择的全局搜索优化计算技术。针对不同问题，通过设计不同的编码方法来表示问题的可行解，采用多种不同的遗传算子来模拟不同环境下的生物遗传特性，以得出全局最优解或较优解。

适应度函数的选择

遗传算法评价染色体优劣的标准就是染色体适应度值。在用遗传算法解决实际应用问题时，需要设计具有针对性的适应度函数。由于在实际生产中，板材切割后剩余废料越少越好，即利用率最大，故本文针将板材利用率，即所有矩形纸箱的面积和除以所占用的板材的总面积，作为就可以衡量切割方案优劣的标准，板材利用率函数为：

$f(i)=\sum_{i=1}^{n}(x_{i},y_{i})/(L \times W)$

其中，$\sum_{i=1}^{n}$为所有矩形纸箱的面积和，$(L \times W)$为所占用的板材的总面积，

适应度的取值范围在[0, 1]之间，适应度值越接近于1，说明个体越优秀，反之，说明个体性能越差，在进行下一步迭代的过程中就可能被淘汰。

遗传操作

（1）初始种群的生成

本文采用十进制编码，设置初始种群大小为20。对于瓦楞板采用”一刀切”的方式进行切割，初始种群生成流程如下：

Step 1：建立坐标系，确定上限宽度与长度，即瓦楞板大小；

Step 2：产生一个随机数序列，取值范围为[1, 12]；

Step 3：根据随机数序列将纸箱按层排列，当大小超出上限后跳出循坏给出编码；

Step 4：重复上述步骤直至产生20个初始个体。

（2）选择

遗传算法中的“选择”是模拟自然界中优胜略汰的自然选择，即从群体中选择优胜的个体，淘汰劣质个体，其目的是把优化的解直接或间接遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的，本文在计算出适应度的基础上进行排序，采用适应度比例方法留下优化的解：

$p=f(i)/\sum_{i=1}^{n}$

其中，$p$为染色体i被选择的概率，$f(i)$为染色体i的适应度，即染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和。

（3）交叉

自然界中生物进化的多样性依靠生物遗传基因的重组或变异，遗传算法中采用交叉算子模拟该过程。交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作，这使得遗传算法的搜索能力得以飞跃提高。本文将交叉概率设置为0.7。

（4）变异

变异的基本内容是对群体中的个体串的某些基因位置上的基因值作变动，是解的进化中产生新个体的辅助方法。变异的目的一是提高算法局部搜索能力，二是使遗传算法可维持群体多样性，以防止出现未成熟收敛现象。本文将变异概率设置为0.1。

终止条件的设置

常见的终止条件设置为，当最优个体的适应度达到给定的阈值，或者最优个体的适应度和群体适应度不再上升时，或者迭代次数达到预设的代数时，算法终止。本文采用设置迭代次数的方式进行终止，迭代次数为100次。

图3 遗传算法流程图

遗传算法模型的求解

将预处理的数据带入到建立的模型中求解，最终得到各瓦楞板利用率较高的几种使用方式(表2)。

表2 各瓦楞板切割方式

切割方式编号	1	2	3	4	5	6	7	8
瓦楞板边长	2500	2500	2500	2500	2000	2000	2000	1800
提供1号纸箱数目	2	0	0	0	0	0	0	0
提供2号纸箱数目	0	2	0	0	0	0	0	0
提供3号纸箱数目	0	0	3	0	0	0	0	0
提供4号纸箱数目	0	0	0	0	3	0	3	0
提供5号纸箱数目	0	4	0	0	3	0	0	0
提供6号纸箱数目	0	0	0	15	0	6	0	0
提供7号纸箱数目	0	0	3	0	0	0	0	6
提供8号纸箱数目	0	1	0	0	1	2	0	2
提供9号纸箱数目	0	0	12	0	0	0	0	0
提供10号纸箱数目	8	0	0	0	0	6	0	5
提供11号纸箱数目	0	11	0	0	0	0	14	1
提供12号纸箱数目	14	0	1	0	0	0	0	0
利用率	96.13%	95.10%	98.33%	92.16%	91.02%	92.16%	93.69%	99.54%

切割方式编号	1	2	3	4	5	6	7	8
瓦楞板边长	2500	2500	2500	2500	2000	2000	2000	1800
提供1号纸箱数目	2	0	0	0	0	0	0	0
提供2号纸箱数目	0	2	0	0	0	0	0	0
提供3号纸箱数目	0	0	3	0	0	0	0	0
提供4号纸箱数目	0	0	0	0	3	0	3	0
提供5号纸箱数目	0	4	0	0	3	0	0	0
提供6号纸箱数目	0	0	0	15	0	6	0	0
提供7号纸箱数目	0	0	3	0	0	0	0	6
提供8号纸箱数目	0	1	0	0	1	2	0	2
提供9号纸箱数目	0	0	12	0	0	0	0	0
提供10号纸箱数目	8	0	0	0	0	6	0	5
提供11号纸箱数目	0	11	0	0	0	0	14	1
提供12号纸箱数目	14	0	1	0	0	0	0	0
利用率	96.13%	95.10%	98.33%	92.16%	91.02%	92.16%	93.69%	99.54%

基于整数线性规划的生产规模规划

在完成切割方式的确定后，接下来对生产规模进行整数线性规划[5~6]。

对于线性规划模型的建立，首先考虑需求量的约束，在上述遗传算法中，我们已得到了每种模式具体的生产每种箱子的数量，则可知每种生产模式与生产数量之积的和可以代表实际生产量，对此我们建立了实际生产量 < 需求量的约束；接下来对目标函数$z$(利润)进行建立，即箱子售价总和与成本之差再加上回收费用，并求其在需求量约束下的最大值。

$max\ z = \sum_{i = 1}^{M}d_{i} \cdot m_{i} - \sum_{j=1}^{N}x_{j} \cdot c_{j} + m_{re} \cdot (\sum_{j = 1}^{N}x_{j} \cdot a_{j}^{2}-\sum_{i=0}^{M}d_{i} \cdot l_{i} \cdot w_{i})$

需满足的约束条件：

1、各类纸箱生产数量大于其需求量：$A \dot x_{i} \geq d_{i}$

2、切割模式的使用次数为非负整数：$x_{i}$为整数，$x_{i} \leq 0$

三层纸箱需求量约束方程组如下所示：

$\begin{cases}2\times x_1+2\times x_{14} \geq 40\\ 2\times x_2+2\times x_{15}\geq 67\\ 3\times x_3+2\times x_{16}\geq 86\\ 3\times x_5+3\times x_7+2\times x_{13}\geq 89\\ 4\times x_2+3\times x_5+2\times x_{11}\geq 108\\ 15\times x_4+6\times x_6+\geq 111\\ 3\times x_3+6\times x_8+4\times x_{11}+4\times x_{16}\geq 123\\ x_2+x_5+2\times x_6+2\times x_8+10\times x_9\geq 129\\ 12\times x_3+15\times x_{10}+3\times x_{16}\geq 140\\ 8\times x_1+6\times x_6+5\times x_8+6\times x_9+8*x_{12}+3\times x_{14}+x_{16}\geq 110\\ 11\times x_2+14\times x_7+x_8+2\times x_{12}\geq 96\\ 14\times x_1+x_3+8\times x_{11}+6\times x_{12}+6\times x_{13}\end{cases}$

使用python中的pulp库函数求解，得到最终结果如下表所示：

表3 问题一线性规划求解结果

切割方式编号	三层瓦楞板对应切割方式使用次数	五层瓦楞板对应切割方式使用次数
1	0	0
2	1	2
3	28	26
4	7	6
5	24	21
6	1	0
7	6	4
8	1	0
9	10	6
10	0	0
11	16	0
12	0	0
13	0	0
14	20	43
15	33	46
16	1	1

求得三层纸箱总利润约为239.599元，原料利用率约为81.08%；五层纸箱总利润约为176.87元，原料利用率约为78.67%，利润总计约416.469元。

问题二模型的建立与求解

问题二的分析

问题二在问题一的基础上进行了调整，增加了的纸箱在容积误差 30%之内可以以大纸箱代替小纸箱供货的条件，其中怎样进行生产计划的弹性调整是解决问题的关键。为了解决这个问题，本文首先求出容积差在30%以内的纸箱，其次，采取递推策略，将小纸箱的需求设置为原需求-被替换数，之后利用线性规划进行求解。

问题二模型的建立

首先通过计算，我们找出了容积差在30%以内的可替换策略共有4种，分别为5号替换6号纸箱，6号替换7号纸箱，8号替换9号纸箱和11号替换12号纸箱。

在问题一的线性规划基础上，增加变量$I_{p,q}$表示实际生产中包装$p$由包装$q$代替的数量，由于此时的生产纸箱数量并不是需求数量，而是原有需求数量-由其他纸箱替代数量+替代其他纸箱数量，表达为原有的$d_{i}$替换为$(d_{i}-\sum_{q=1}^{M}I_{i,q}+\sum_{p=1}^{M}I_{p,i})$。

新建立的利润最大化目标函数如下：

$max\ z = \sum_{i = 1}^{M}(d_{i}-\sum_{q=1}^{M}I_{i,q}+\sum_{p=1}^{M}I_{p,i}) \cdot m_{i} - \sum_{j=1}^{N}x_{j} \cdot c_{j} + m_{re} \cdot [\sum_{j = 1}^{N}x_{j} \cdot a_{j}^{2}-\sum_{i=0}^{M}(d_{i}-\sum_{q=1}^{M}I_{i,q}+\sum_{p=1}^{M}I_{p,i}) \cdot l_{i} \cdot w_{i}]$

满足的约束条件为：

各类纸箱生产数量大于其需求量：$A \cdot x_{i} \geq d_{i} - \sum_{q=1}^{M}I_{p,q}+\sum_{p=1}^{M}I_{p.i}$
切割模式的使用次数为非负整数：$x_{i}$为整数，$x \geq 0$

建立相关三层纸箱需求量线性规划约束方程组如下：

$\begin{cases}2\times x_1+2\times x_{14} \geq 40\\2\times x_2+2\times x_{15}\geq 67\\ 3\times x_3+2\times x_{16}\geq 86\\ 3\times x_5+3\times x_7+2\times x_{13}\geq 89\\ 4\times x_2+3\times x_5+2\times x_{11}\geq 108+I_{5,6}\\ 15\times x_4+6\times x_6+\geq 111-I_{5,6}+I_{6,7}\\ 3\times x_3+6\times x_8+4\times x_{11}+4\times x_{16}\geq 123-I_{6,7}\\ x_2+x_5+2\times x_6+2\times x_8+10\times x_9\geq 129+I_{8,9}\\ 12\times x_3+15\times x_{10}+3\times x_{16}\geq 140-I_{8,9}\\ 8\times x_1+6\times x_6+5\times x_8+6\times x_9+8*x_{12}+3\times x_{14}+x_{16}\geq 110\\ 11\times x_2+14\times x_7+x_8+2\times x_{12}\geq 96+I_{11,12}\\ 14\times x_1+x_3+8\times x_{11}+6\times x_{12}+6\times x_{13}\end{cases}$

问题二模型的求解

根据以上建立的相关方程组，使用python中的pulp库函数求解，得到最优生产计划如下表所示：

表4 问题二线性规划求解结果

切割方式编号	三层瓦楞板对应切割方式使用次数	五层瓦楞板对应切割方式使用次数
1	0	0
2	0	5
3	28	26
4	0	4
5	23	24
6	0	0
7	7	1
8	0	0
9	11	5
10	0	0
11	75	0
12	0	0
13	0	0
14	20	43
15	34	43
16	1	1

并解得最优替换策略如下表所示：

表5 最大利润下的替换策略

替换方法	三层纸箱	五层纸箱
5号替换6号次数	111	22
6号替换7号次数	0	0
8号替换9号次数	4	0
11号替换12号次数	2	4

其中三层纸箱总利润约为243.089元，利用率约为67.78%；五层纸箱总利润约为181.425元，利用率约为79.86%。利润合计约为424.514元。

问题三模型的建立与求解

问题三的分析

问题三要求求出哪一种快递纸箱的需求变化量对生产计划最敏感。在这里我们利用生产总利润代表生产计划，这样不仅可以使该问题能够在上述模型的基础上进行求解，而且结果直观准确，能够直接地反映出各纸箱需求量变化对生产计划的敏感度。为了体现各纸箱对于生产需求的敏感度，本文采用控制变量法，分别将各个纸箱的需求量提高10%，后带入到问题一建立的线性规划模型中求解最优生产计划下的总利润，设置目标函数为利润变化率对其进行灵敏度分析[7]。

灵敏度分析

在各纸箱需求量大小的情况下根据问题一的模型解出最大利润，并求出最大利润变化率，得到结果如下：

三层：
原利润为：239.599360
第1个纸箱需求量增加10%后，利润变为249.439360，变化率为0.041069
第2个纸箱需求量增加10%后，利润变为252.067360，变化率为0.052037
第3个纸箱需求量增加10%后，利润变为250.279360，变化率为0.044574
第4个纸箱需求量增加10%后，利润变为248.949360，变化率为0.039023
第5个纸箱需求量增加10%后，利润变为248.479360，变化率为0.037062
第6个纸箱需求量增加10%后，利润变为247.149360，变化率为0.031511
第7个纸箱需求量增加10%后，利润变为247.759360，变化率为0.034057
第8个纸箱需求量增加10%后，利润变为245.865360，变化率为0.026152
第9个纸箱需求量增加10%后，利润变为246.599360，变化率为0.029215
第10个纸箱需求量增加10%后，利润变为243.889360，变化率为0.017905
第11个纸箱需求量增加10%后，利润变为242.325360，变化率为0.011377
第12个纸箱需求量增加10%后，利润变为241.919360，变化率为0.009683

五层：
原利润为：176.870300
第1个纸箱需求量增加10%后，利润变为195.710300，变化率为0.106519
第2个纸箱需求量增加10%后，利润变为195.434300，变化率为0.104958
第3个纸箱需求量增加10%后，利润变为183.520300，变化率为0.037598
第4个纸箱需求量增加10%后，利润变为184.436300，变化率为0.042777
第5个纸箱需求量增加10%后，利润变为183.678300，变化率为0.038491
第6个纸箱需求量增加10%后，利润变为185.430300，变化率为0.048397
第7个纸箱需求量增加10%后，利润变为182.910300，变化率为0.034149
第8个纸箱需求量增加10%后，利润变为180.320300，变化率为0.019506
第9个纸箱需求量增加10%后，利润变为180.710300，变化率为0.021711
第10个纸箱需求量增加10%后，利润变为180.050300，变化率为0.017979
第12个纸箱需求量增加10%后，利润变为179.450300，变化率为0.014587
第12个纸箱需求量增加10%后，利润变为179.460300，变化率为0.014643

可以看出，需求量分别增加10%后，1号和2号纸箱的利润变化率较大，说明其对需求量较为灵敏。除此之外，其余纸箱利润率变化基本在5%以下，最大的也仅在10%左右，说明系统稳定性良好，灵敏度检验效果较好。

模型的优缺点

模型优点

遗传算法[8]作为现代优化算法之一，有着一定的优点，如：能够求出优化问题的全局最优解；优化结果与初始条件无关；算法独立于求解域；具有较强的鲁棒性；适合于求解复杂的优化问题；应用较为广泛。

而线性规划是决策系统的静态最优化数学规划方法之一，在现代决策中的应用是非常广泛的，它可以在各种相互关联的多变量约束条件下,解决或规划一个对象的线性目标函数最优的问题，非常适用于本题。

因此，本文建立的数学模型不仅适用范围广，而且结果准确。

模型缺点

遗传算法收敛速度慢，局部搜索能力差。并且染色体数、交叉概率、变异概率、终止条件都需一定的主观性判断，需经多次实验才可找到较优解。

而线性规划是一个静态模型，随着条件的改变，约束条件与目标函数可能都要随之进行调整，这种机械性决定它在某种意义上不可避免的局限性。

参考文献

[1] 瓦楞纸箱需求增长趋势[J]. 中国包装, 2019, 39(03):86.

[2] 马俊燕, 韩志会, 骆德铖, 韩贺春, 肖海华. 不确定环境下一维下料问题[J]. 锻压技术, 2020, 45(03):190-196.

[3] 田康. 基于遗传算法对二维下料问题的研究[J]. 科技风, 2020(09):198.

[4] 朱艳华. 瓦楞纸板生产线的工艺控制和标准化[J]. 印刷技术, 2017(07):51-53.

[5] 王茹, 黄亚辉. 线性规划在实际生产生活中的应用[J]. 科技创新导报, 2018, 15(09):155-156.

[6] 姚凯翊. 线性规划在企业生产中的案例研究[J]. 现代商业, 2020(17):108-109.

[7] 勒晓阳, 李松仁, 贾春霖. 线性规划灵敏度分析模型[J]. 中南矿冶学院学报, 1990(06):602-609.

[8] 唐文琦, 曾干敏, 刘泽宇. 浅谈遗传算法及其部分改进算法[J]. 科技风, 2019(12):57.

附录

数据预处理相关python代码 data_process.py

import math
import random
import numpy as np
import sko
from sko.GA import GA

box = [[530, 300, 370], [530, 240, 290],
       [430, 210, 270], [350, 190, 230],
       [290, 170, 190], [250, 150, 180],
       [230, 130, 160], [210, 110, 140],
       [195, 105, 135], [175, 95, 115],
       [145, 85, 105], [130, 80, 90]]
box_need_three = [40, 67, 86, 89, 108, 111,
                  123, 129, 140, 110, 96, 84]
box_need_five = [85, 95, 80, 75, 70, 82,
                 76, 79, 69, 60, 65, 78]
box_price_three = [2.91, 2.21, 1.76, 1.35, 1.02, 0.80,
                   0.68, 0.55, 0.50, 0.39, 0.34, 0.29]
box_price_five = [3.78, 2.82, 2.25, 1.71, 1.30, 1.07,
                  0.87, 0.70, 0.64, 0.53, 0.43, 0.37]
board = [2500, 2000, 1800, 1500]
board_price_three = [10, 6.5, 4.8, 4.0]
board_price_five = [(x * 1.3) for x in board_price_three]

arr = []
for boxx in box:
    arr.append([2 * (boxx[0] + boxx[1]), 2 * boxx[1] + boxx[2]])
# print(arr)

q = 1.4
sum_three = 0
all_three = 0
sum_five = 0
all_five = 0
delta_three = []
delta_five = []
all_instead_three = 0
all_instead_five = 0
for i in range(len(box)):
    if i == 4:
        all_instead_three += arr[i][0] * arr[i][1] * (box_need_three[i] + 111)
    elif i == 5:
        k = 0
    elif i == 7:
        all_instead_three += arr[i][0] * arr[i][1] * (box_need_three[i] + 4)
    elif i == 8:
        all_instead_three += arr[i][0] * arr[i][1] * (box_need_three[i] - 4)
    elif i == 10:
        all_instead_three += arr[i][0] * arr[i][1] * (box_need_three[i] + 2)
    elif i == 11:
        all_instead_three += arr[i][0] * arr[i][1] * (box_need_three[i] - 2)
    else:
        all_instead_three += arr[i][0] * arr[i][1] * box_need_three[i]
    if i == 4:
        all_instead_five += arr[i][0] * arr[i][1] * (box_need_five[i] + 22)
    elif i == 5:
        all_instead_five += arr[i][0] * arr[i][1] * (box_need_five[i] - 22)
    elif i == 10:
        all_instead_five += arr[i][0] * arr[i][1] * (box_need_five[i] + 4)
    elif i == 11:
        all_instead_five += arr[i][0] * arr[i][1] * (box_need_five[i] - 4)
    else:
        all_instead_five += arr[i][0] * arr[i][1] * box_need_five[i]
    delta_three.append(box_price_three[i] - q * arr[i][0] * arr[i][1] * 1e-6)
    delta_five.append(box_price_five[i] - q * arr[i][0] * arr[i][1] * 1e-6)
    all_five += arr[i][0] * arr[i][1] * box_need_five[i]
    sum_five += box_need_five[i] * (box_price_five[i] - q * arr[i][0] * arr[i][1] * 1e-6)
    all_three += arr[i][0] * arr[i][1] * box_need_three[i]
    sum_three += box_need_three[i] * (box_price_three[i] - q * arr[i][0] * arr[i][1] * 1e-6)
# print(sum_three)
# print(all_three)
# print(sum_five)
# print(all_five)

Volume = []
for i in range(len(box)):
    Volume.append(box[i][0] * box[i][1] * box[i][2])
# print(Volume)

instead = []
for i in range(len(Volume)):
    temp = []
    for j in range(i):
        if (Volume[j] - Volume[i]) / Volume[j] < 0.3:
            temp.append(j)
    instead.append(temp)
# print(instead)

# print(delta_three)
# print(delta_five)
print(all_instead_three)
print(all_instead_five)

问题一线性规划模型相关python代码 FirstProblemSolve.py

from pulp import *

size = {'x1': 2500, 'x2': 2500, 'x3': 2500, 'x4': 2500, 'x5': 2000, 'x6': 2000, 'x7': 2000, 'x8': 1800,
        'x9': 1800, 'x10': 1800, 'x11': 1800, 'x12': 1500, 'x13': 1500, 'x14': 2000, 'x15': 1800, 'x16': 2000}


def solve(con, all_need, sum_get, c):
    prob = LpProblem('myPro', LpMinimize)
    x1 = LpVariable('x1', lowBound=0, cat='Integer')
    x2 = LpVariable('x2', lowBound=0, cat='Integer')
    x3 = LpVariable('x3', lowBound=0, cat='Integer')
    x4 = LpVariable('x4', lowBound=0, cat='Integer')
    x5 = LpVariable('x5', lowBound=0, cat='Integer')
    x6 = LpVariable('x6', lowBound=0, cat='Integer')
    x7 = LpVariable('x7', lowBound=0, cat='Integer')
    x8 = LpVariable('x8', lowBound=0, cat='Integer')
    x9 = LpVariable('x9', lowBound=0, cat='Integer')
    x10 = LpVariable('x10', lowBound=0, cat='Integer')
    x11 = LpVariable('x11', lowBound=0, cat='Integer')
    x12 = LpVariable('x12', lowBound=0, cat='Integer')
    x13 = LpVariable('x13', lowBound=0, cat='Integer')
    x14 = LpVariable('x14', lowBound=0, cat='Integer')
    x15 = LpVariable('x15', lowBound=0, cat='Integer')
    x16 = LpVariable('x16', lowBound=0, cat='Integer')
    X = [x1, x2, x3, x4, x5, x6, x7, x8,
         x9, x10, x11, x12, x13, x14, x15, x16]

    z = 0
    for i in range(len(X)):
        z += X[i] * c[i]
    prob += z

    prob += 2 * x1 + 2 * x14 >= con[0]
    prob += 2 * x2 + 2 * x15 >= con[1]
    prob += 3 * x3 + 2 * x16 >= con[2]
    prob += 3 * x5 + 3 * x7 + 2 * x13 >= con[3]
    prob += 4 * x2 + 3 * x5 + 2 * x11 >= con[4]
    prob += 15 * x4 + 6 * x6 >= con[5]
    prob += 3 * x3 + 6 * x8 + 4 * x11 + 4 * x16 >= con[6]
    prob += x2 + x5 + 2 * x6 + 2 * x8 + 10 * x9 >= con[7]
    prob += 12 * x3 + 15 * x10 + 3 * x16 >= con[8]
    prob += 8 * x1 + 6 * x6 + 5 * x8 + 6 * x9 + 8 * x12 + 3 * x14 + x16 >= con[9]
    prob += 11 * x2 + 14 * x7 + x8 + 2 * x12 >= con[10]
    prob += 14 * x1 + x3 + 8 * x11 + 6 * x12 + 6 * x13 + 7 * x15 >= con[11]

    status = prob.solve()
    print('总利润：', sum_get - value(prob.objective))  # 计算结果
    sum = 0
    for i in prob.variables():
        sum += size[i.name] * size[i.name] * i.varValue
        print(i.name, ": ", i.varValue)
    print('需要面积：', all_need)
    print('使用面积：', sum)
    print('利用率：', all_need / sum)


c_three = [1.25, 1.25, 1.25, 1.25, 0.9, 0.9, 0.9, 0.264,
           0.264, 0.264, 0.264, 0.85, 0.85, 0.9, 0.264, 0.9]
c_five = [4.25, 4.25, 4.25, 4.25, 2.8500000000000014, 2.8500000000000014, 2.8500000000000014, 1.7040000000000006, 1.7040000000000006, 1.7040000000000006,
          1.7040000000000006, 2.0500000000000003, 2.0500000000000003, 2.8500000000000014, 1.7040000000000006, 2.8500000000000014]
con_three = [40, 67, 86, 89, 108, 111,
             123, 129, 140, 110, 96, 84]
con_five = [85, 95, 80, 75, 70, 82,
            76, 79, 69, 60, 65, 78]
all_need_three = 508707600
sum_get_three = 347.23936000000003
all_need_five = 516965500
sum_get_five = 606.6283
print("三层：")
solve(con_three, all_need_three, sum_get_three, c_three)
print("\n")
print("五层：")
solve(con_five, all_need_five, sum_get_five, c_five)

问题一遗传算法模型相关javascript代码 GA.html

<!DOCTYPE >
<html>
	<head>
		<meta charset="utf-8"/>
		<title></title>
	</head>
	<body>
		<button type="button" id="button">计算结果</button>
		<script type="text/javascript">
			var totalNum = 50, // 种群中染色体的总数
			width=2500,//毛坯的宽
			length=2500,//毛坯的长
			N,//记录需要的毛坯数量
            bit = 1183, // 基因数为20位
            total = new Array(); // 种群中的染色体
            bestFitness = 0, // 最佳适应值
            generation = 0, // 染色体代号
            bestGeneration = 0, // 最好的一旦染色体代号
            bestStr = ''; // 最好的染色体基因序列
            var size=[[1660, 970], [1540, 770], [1280, 690], [1080, 610], [920, 530], [800, 480], 
 [720, 420], [640, 360], [600, 345], [540, 305], [460, 275], [420, 250]];//记录小矩形块的长宽
            var num=[40, 67, 86, 89, 108, 111,
                  123, 129, 140, 110, 96, 84]; //记录小矩形块的需求数量
            var sizeTotal = [];
            /*将基因组对应的小矩形块的长宽记录下来*/
            var cnt = 0;
			var sum = 0;
            var pre = [];
            for(var i = 0; i < num.length; ++i) {
                for(var j = 0; j < num[i]; ++j) {
                    sizeTotal.push(size[i]);
                    pre.push(i);
                }
				sum += size[i][0] * size[i][1] * num[i];
            }
            /*初始化一条染色体*/
            function initChar() {
				var arr = [];
        		for(var i=0;i<bit;i++){
            		getx(arr);
        		}	
        		function getx(arr){
            		for(var i=0;i>-1;i++){
                		var flag = true;
                		var num = Math.floor(Math.random()*sizeTotal.length);
                		for(var i in arr){
                    		if(arr[i] == num){
                        		flag= false;
                        		break;
                    		}
                		}
                		if(flag == true){
                    	arr.push(num);
                    	return;
                		}
            		}
        		}return arr;
        	}
            /*初始化一个种群*/
            function initTotal() {
	            for(var i=0;i<totalNum;i++){
	                total[i] = initChar();
	            }
	            return total;
	        }
            
            /*找出数组中的最大值*/
			function findMax(tmp){
				var max = tmp[0];
				for(var i=1;i<tmp.length;i++){ 
					if(max<=tmp[i]){
						max=tmp[i];
					}
				}return max;
	       	}
			
			/*找出数组中的最小值*/
			function findMin(tmp){
	        	var min=tmp[0];
	        	var index=0;
	        	for(var i=1;i<tmp.length;i++){
	        		if(min>tmp[i]){
	        			min=tmp[i];
	        			index=i;
	        		}
	        	}
	        	return min;
	        }
			
			/*找出数组中最小值的index*/
			function findMaxIndex(tmp){
	        	var max=tmp[0];
	        	var index=0;
	        	for(var i=1;i<tmp.length;i++){
	        		if(max<tmp[i]){
	        			max=tmp[i];
	        			index=i;
	        		}
	        	}
	        	return index;
	        }
			
			/*计算适应度函数（也是直接计算需要的矩形块数量）*/
			function calculateFitness(arr) {
				var newArr=[];//记录每一行的矩形块的宽
	            var addLenght=0;//累计长
	            var remLength=0;//剩余长
				var fitness=0;
				var n=0;//累计在出现addLenght>length的情况时i循环的次数的个数
				var neededNum=0;
	            var index1,index2;
	            var count=0;//记录是否出现每行的remLenth还能再放一个矩形块的情况
                var use = 0;
				for(var i=0;i<arr.length;i++){
                    use += sizeTotal[arr[i]][0] * sizeTotal[arr[i]][1];
	            	addLenght+=sizeTotal[arr[i]][0];
	            	n++;
	            	if(addLenght>length){
	            		if(i<n){
	            			for(var j=0;j<i;j++){
				            	newArr[j]=sizeTotal[arr[j]][1];
				            }
	            		}else{
	            			for(var j=0;j<i;j++){
				            	newArr[j]=sizeTotal[arr[j]][1];
				            }
	            			for(var a=0;a<i-n;a++){
				            	newArr.shift();
				            }
	            		}
	            		remLength=length+sizeTotal[arr[i]][0]-addLenght;
	            		if(remLength>5){
	            			outerMost://定义外层循环
	            			for(var m=i;m<arr.length;m++){
	            				for(var h=0;h<2;h++){
	            					if( sizeTotal[arr[m]][h] <= remLength){
	            						index1=m;
		            					index2=h;
					            		count=1;
					            		if(index2==0){
					            			newArr.push(sizeTotal[arr[index1]][1]);
					            		}else{
					            			newArr.push(sizeTotal[arr[index1]][0]);
					            		}
					            		if(index1!=i){
					            			arr.splice(i,0,arr[index1]);
					            			arr.splice(index1+1,1);
					            		}
					            		if(i<arr.length-1){
					        				i++;
					            		}
		            					break outerMost;//终止外层循环
	            					}
	            				}
	            			}
	            		}
			            fitness+=findMax(newArr);
	            		addLenght=sizeTotal[arr[i]][0];
	            		n=0;
	            	}
	            	var newArrRest=[];//储存排在最后一行的矩形块的宽
	            	if(i==arr.length-1){
						if(count==0){
							for(var z=0;z<arr.length;z++){
								newArrRest[z]=sizeTotal[arr[z]][1];
							}
							for(var b=0;b<i-n;b++){
								newArrRest.shift();
							}							
							fitness+=findMax(newArrRest);
						}else{
							for(var z=0;z<arr.length;z++){
								newArrRest[z]=sizeTotal[arr[z]][1];
							}
							for(var b=0;b<i-n-1;b++){
								newArrRest.shift();
							}							
							fitness+=findMax(newArrRest);
						}
					}
	            	if(fitness>width){
	            		neededNum++;
	            		fitness=findMax(newArr);
                        break;
					}
	            	count=0;
	            }
	          	return (length * width) / use;
	        }
			
			/*轮盘赌选择*/
			function select() {
	            var evals = new Array(totalNum); // 所有染色体适应值 
	            var p = new Array(totalNum); // 各染色体选择概率
	            var q = new Array(totalNum); // 累计概率
	            var F = 0; // 累计适应值总合
	            for(var i=0;i<totalNum;i++){ // 记录下种群的最优解
	                evals[i] = calculateFitness(total[i]);
	                if(evals[i] > bestFitness) {
	                    bestFitness = evals[i];
	                    bestStr = total[i];
	                }
	                F += evals[i];
	            }
	            for(var j=0;j<totalNum;j++){ // 计算累计概率
	                p[j] = evals[j]/F;
	                if(j == 0){
	                    q[j] = p[j];
	                }
	                else{
	                    q[j]=q[j-1]+p[j];
	                }
	            }
	            var temp = new Array(totalNum);
	            for(var k=0;k<totalNum;k++){ //
	                var r = Math.random();
	                if(r <= q[0]){
	                    temp = total[0];
	                    break;
	                }
	                else{
	                    for(var z=1;z<totalNum;z++){
	                        if(r<q[z]){
	                            temp = total[z];
	                            break;
	                        }
	                    }
	                }
	            }
	            return temp;
	        }
			
			
			/*染色体交叉
			 *交叉概率为70%
			 */
			function jiaocha(population1,population2){
				var returnPopulation1 = new Array(bit);
				var returnPopulation2 = new Array(bit);
				var temp=Math.random();
				if(temp<0.7){
					for(var i=0;i<bit;i++){
						if(i<bit-2){
							returnPopulation1[i]=population1[i];
							returnPopulation2[i]=population2[i];
						}else{
							returnPopulation1[i]=population2[i];
							returnPopulation2[i]=population1[i];
						}
					}
					//找出重合的基因,并将相同基因改正
					for(var j=bit-1;j>bit-3;j--){
						for(var k=0;k<bit-2;k++){
							if(returnPopulation1[k]==returnPopulation1[j]){
								returnPopulation1[k]=returnPopulation2[j];
							}
						}
					}
				}else{
					returnPopulation1=population1;
					returnPopulation2=population2;
				}
				return returnPopulation1;
			}
			
			/*染色体变异*/
			function change(arr) {
	            if(Math.random()<0.1){
	            	while(1){
	            		var temp1=parseInt(Math.random()*bit);
	            		var temp2=parseInt(Math.random()*bit);
	            		if(temp1!=temp2){
	            			break;
	            		}
	            	}
	            	var temp=arr[temp1];
	            	arr[temp1]=arr[temp2];
	            	arr[temp2]=temp;
	            }
	            return arr;
	        }
			/*执行过程*/
	        var d1 = new Date();
			document.getElementById('button').onclick = function () {
	            total = initTotal();
	            var arr=[];
	            var bestArr=[];
	            for(var i=0;i<10000;i++){
	            	bestArr[i]=change(jiaocha(select(),select()));
	            	arr[i] = calculateFitness(bestArr[i]);
	            }
	            //var minFitness=findMin(arr);
	            //bestStr = bestArr[findMaxIndex(arr)];
	            //console.log(bestStr);
	            console.log(1 / calculateFitness(bestStr));
	            var d2 = new Date();
	            var time=d2-d1;
	            console.log('一共执行了'+time+'ms');
	        }
		</script>
	</body>
</html>

问题二线性规划模型相关python代码 SecondProblemSolve.py

from pulp import *

size = {'x1': 2500, 'x2': 2500, 'x3': 2500, 'x4': 2500, 'x5': 2000, 'x6': 2000, 'x7': 2000, 'x8': 1800,
        'x9': 1800, 'x10': 1800, 'x11': 1800, 'x12': 1500, 'x13': 1500, 'x14': 2000, 'x15': 1800, 'x16': 2000}


def solve(con, all_need, sum_get, c, delta):
    prob = LpProblem('myPro', LpMinimize)
    x1 = LpVariable('x1', lowBound=0, cat='Integer')
    x2 = LpVariable('x2', lowBound=0, cat='Integer')
    x3 = LpVariable('x3', lowBound=0, cat='Integer')
    x4 = LpVariable('x4', lowBound=0, cat='Integer')
    x5 = LpVariable('x5', lowBound=0, cat='Integer')
    x6 = LpVariable('x6', lowBound=0, cat='Integer')
    x7 = LpVariable('x7', lowBound=0, cat='Integer')
    x8 = LpVariable('x8', lowBound=0, cat='Integer')
    x9 = LpVariable('x9', lowBound=0, cat='Integer')
    x10 = LpVariable('x10', lowBound=0, cat='Integer')
    x11 = LpVariable('x11', lowBound=0, cat='Integer')
    x12 = LpVariable('x12', lowBound=0, cat='Integer')
    x13 = LpVariable('x13', lowBound=0, cat='Integer')
    x14 = LpVariable('x14', lowBound=0, cat='Integer')
    x15 = LpVariable('x15', lowBound=0, cat='Integer')
    x16 = LpVariable('x16', lowBound=0, cat='Integer')
    I56 = LpVariable('I56', lowBound=0, upBound=con[5], cat='Integer')
    I67 = LpVariable('I67', lowBound=0, upBound=con[6], cat='Integer')
    I89 = LpVariable('I89', lowBound=0, upBound=con[8], cat='Integer')
    I1112 = LpVariable('I1112', lowBound=0, upBound=con[11], cat='Integer')
    X = [x1, x2, x3, x4, x5, x6, x7, x8,
         x9, x10, x11, x12, x13, x14, x15, x16]

    z = 0
    for i in range(len(c)):
        z += X[i] * c[i]
    z += I56 * (delta[5] - delta[4])
    z += I67 * (delta[6] - delta[5])
    z += I89 * (delta[8] - delta[7])
    z += I1112 * (delta[11] - delta[10])
    prob += z

    prob += 2 * x1 + 2 * x14 >= con[0]
    prob += 2 * x2 + 2 * x15 >= con[1]
    prob += 3 * x3 + 2 * x16 >= con[2]
    prob += 3 * x5 + 3 * x7 + 2 * x13 >= con[3]
    prob += 4 * x2 + 3 * x5 + 2 * x11 - I56 >= con[4]
    prob += 15 * x4 + 6 * x6 + I56 - I67 >= con[5]
    prob += 3 * x3 + 6 * x8 + 4 * x11 + 4 * x16 + I67 >= con[6]
    prob += x2 + x5 + 2 * x6 + 2 * x8 + 10 * x9 - I89 >= con[7]
    prob += 12 * x3 + 15 * x10 + 3 * x16 + I89 >= con[8]
    prob += 8 * x1 + 6 * x6 + 5 * x8 + 6 * x9 + 8 * x12 + 3 * x14 + x16 >= con[9]
    prob += 11 * x2 + 14 * x7 + x8 + 2 * x12 - I1112 >= con[10]
    prob += 14 * x1 + x3 + 8 * x11 + 6 * x12 + 6 * x13 + 7 * x15 + I1112 >= con[11]

    status = prob.solve()
    print('总利润：', sum_get - value(prob.objective))  # 计算结果
    sum = 0
    cnt = 0
    all = 0
    for i in prob.variables():
        if cnt >= 4:
            sum += size[i.name] * size[i.name] * i.varValue
        print(i.name, ": ", i.varValue)
        cnt += 1
    print('需要面积：', all_need)
    print('使用面积：', sum)
    print('利用率：', all_need / sum)


c_three = [1.25, 1.25, 1.25, 1.25, 0.9, 0.9, 0.9, 0.264,
           0.264, 0.264, 0.264, 0.85, 0.85, 0.9, 0.264, 0.9]
c_five = [4.25, 4.25, 4.25, 4.25, 2.8500000000000014, 2.8500000000000014, 2.8500000000000014,
          1.7040000000000006, 1.7040000000000006, 1.7040000000000006, 1.7040000000000006, 2.0500000000000003,
          2.0500000000000003, 2.8500000000000014, 1.7040000000000006, 2.8500000000000014]
con_three = [40, 67, 86, 89, 108, 111,
             123, 129, 140, 110, 96, 84]
con_five = [85, 95, 80, 75, 70, 82,
            76, 79, 69, 60, 65, 78]
delta_three = [0.6557200000000001, 0.5498800000000001, 0.52352, 0.42768000000000017, 0.33736, 0.2624000000000001,
               0.25664000000000015, 0.2274400000000001, 0.2102, 0.15942000000000003, 0.16290000000000004, 0.143]
delta_five = [1.5257199999999997, 1.15988, 1.01352, 0.78768, 0.61736,
              0.5324000000000001, 0.4466400000000001, 0.37744, 0.3502, 0.29942, 0.2529, 0.223]
all_need_three = 508707600
sum_get_three = 347.23936000000003
all_need_five = 516965500
sum_get_five = 606.6283
print("三层：")
solve(con_three, all_need_three, sum_get_three, c_three, delta_three)
print("\n")
print("五层：")
solve(con_five, all_need_five, sum_get_five, c_five, delta_five)

问题三灵敏度分析模型相关python代码 ThirdProblemSolve.py

from pulp import *
import math

size = {'x1': 2500, 'x2': 2500, 'x3': 2500, 'x4': 2500, 'x5': 2000, 'x6': 2000, 'x7': 2000, 'x8': 1800,
        'x9': 1800, 'x10': 1800, 'x11': 1800, 'x12': 1500, 'x13': 1500, 'x14': 2000, 'x15': 1800, 'x16': 2000}


def solve(con, all_need, sum_get, c):
    prob = LpProblem('myPro', LpMinimize)
    x1 = LpVariable('x1', lowBound=0, cat='Integer')
    x2 = LpVariable('x2', lowBound=0, cat='Integer')
    x3 = LpVariable('x3', lowBound=0, cat='Integer')
    x4 = LpVariable('x4', lowBound=0, cat='Integer')
    x5 = LpVariable('x5', lowBound=0, cat='Integer')
    x6 = LpVariable('x6', lowBound=0, cat='Integer')
    x7 = LpVariable('x7', lowBound=0, cat='Integer')
    x8 = LpVariable('x8', lowBound=0, cat='Integer')
    x9 = LpVariable('x9', lowBound=0, cat='Integer')
    x10 = LpVariable('x10', lowBound=0, cat='Integer')
    x11 = LpVariable('x11', lowBound=0, cat='Integer')
    x12 = LpVariable('x12', lowBound=0, cat='Integer')
    x13 = LpVariable('x13', lowBound=0, cat='Integer')
    x14 = LpVariable('x14', lowBound=0, cat='Integer')
    x15 = LpVariable('x15', lowBound=0, cat='Integer')
    x16 = LpVariable('x16', lowBound=0, cat='Integer')
    X = [x1, x2, x3, x4, x5, x6, x7, x8,
         x9, x10, x11, x12, x13, x14, x15, x16]

    z = 0
    for i in range(len(X)):
        z += X[i] * c[i]
    prob += z

    prob += 2 * x1 + 2 * x14 >= con[0]
    prob += 2 * x2 + 2 * x15 >= con[1]
    prob += 3 * x3 + 2 * x16 >= con[2]
    prob += 3 * x5 + 3 * x7 + 2 * x13 >= con[3]
    prob += 4 * x2 + 3 * x5 + 2 * x11 >= con[4]
    prob += 15 * x4 + 6 * x6 >= con[5]
    prob += 3 * x3 + 6 * x8 + 4 * x11 + 4 * x16 >= con[6]
    prob += x2 + x5 + 2 * x6 + 2 * x8 + 10 * x9 >= con[7]
    prob += 12 * x3 + 15 * x10 + 3 * x16 >= con[8]
    prob += 8 * x1 + 6 * x6 + 5 * x8 + 6 * x9 + 8 * x12 + 3 * x14 + x16 >= con[9]
    prob += 11 * x2 + 14 * x7 + x8 + 2 * x12 >= con[10]
    prob += 14 * x1 + x3 + 8 * x11 + 6 * x12 + 6 * x13 + 7 * x15 >= con[11]

    prob.solve()
    return sum_get - value(prob.objective)


arr = [[1660, 970], [1540, 770], [1280, 690], [1080, 610], [920, 530], [800, 480],
       [720, 420], [640, 360], [600, 345], [540, 305], [460, 275], [420, 250]]
c_three = [1.25, 1.25, 1.25, 1.25, 0.9, 0.9, 0.9, 0.264,
           0.264, 0.264, 0.264, 0.85, 0.85, 0.9, 0.264, 0.9]
c_five = [4.25, 4.25, 4.25, 4.25, 2.8500000000000014, 2.8500000000000014, 2.8500000000000014, 1.7040000000000006, 1.7040000000000006, 1.7040000000000006,
          1.7040000000000006, 2.0500000000000003, 2.0500000000000003, 2.8500000000000014, 1.7040000000000006, 2.8500000000000014]
con_three = [40, 67, 86, 89, 108, 111,
             123, 129, 140, 110, 96, 84]
con_five = [85, 95, 80, 75, 70, 82,
            76, 79, 69, 60, 65, 78]
all_need_three = 508707600
sum_get_three = 347.23936000000003
all_need_five = 516965500
sum_get_five = 606.6283

box_price_three = [2.91, 2.21, 1.76, 1.35, 1.02, 0.80,
                   0.68, 0.55, 0.50, 0.39, 0.34, 0.29]
box_price_five = [3.78, 2.82, 2.25, 1.71, 1.30, 1.07,
                  0.87, 0.70, 0.64, 0.53, 0.43, 0.37]

Get_three = solve(con_three, all_need_three, sum_get_three, c_three)
Get_five = solve(con_five, all_need_five, sum_get_five, c_five)
get_three_change = []
get_five_change = []
for i in range(len(con_three)):
    con = con_three.copy()
    con[i] = math.floor(con[i] * 1.1)
    sum_get = sum_get_three + box_price_three[i] * (con[i] - con_three[i])
    get_three_change.append(solve(con, all_need_three, sum_get, c_three))
for i in range(len(con_three)):
    con = con_five.copy()
    con[i] = math.floor(con[i] * 1.1)
    sum_get = sum_get_five + box_price_five[i] * (con[i] - con_five[i])
    get_five_change.append(solve(con, all_need_five, sum_get, c_five))

print("三层：")
print("原利润为：%f" % Get_three)
for i in range(len(get_three_change)):
    print("第%d个纸箱需求量增加10%%后，利润变为%f，变化率为%f" % (i, get_three_change[i], (get_three_change[i] - Get_three) / Get_three))

print("\n")
print("五层：")
print("原利润为：%f" % Get_five)
for i in range(len(get_five_change)):
print("第%d个纸箱需求量增加10%%后，利润变为%f，变化率为%f" % (i, get_five_change[i], (get_five_change[i] - Get_five) / Get_five))

摘 要